 |
Effets
sur l'espace temps.
Albert Einstein a été l'artisan d'un
principe fondamental du XX° siècle :
le principe de relativité. Le principe de
la relativité exprime l'idée que les
lois de la physique doivent être identiques
dans tous les référentiels quels qu'ils
soient. En appliquant le principe de la relativité
aux repères galiléens, Einstein bâtit
la théorie de la relativité restreinte.
En cherchant à incorporer la gravitation
dans ses lois relativistes, Einstein découvrit
un lien étroit entre le mouvement d'un référentiel
uniformément accéléré
et un champ gravitationnel. En 1907, une pensée
lui traversa l'esprit. Pour reprendre ses mots :
"J'étais assis à mon bureau à
l'office des brevets à Berne, quand une idée
me vint soudain : si une personne est en chute libre,
elle ne sentira plus son propre poids". Il
l'appela par la suite "la pensée la
plus heureuse de ma vie".
Les conséquences de cette idée furent
bouleversantes. Si vous tombez en chute libre, par
exemple en sautant d'une falaise, non seulement
vous ne sentez plus votre poids, mais il vous semble
que tous les effets de la gravité ont disparu
de votre voisinage. Ainsi, si vous lâchez
des pierres pendant votre chute, elles resteront
à vos cotés pendant la chute. Si vous
ne regardez que ces pierres et ignorez le reste
de l’environnement, vous ne pouvez pas savoir
si les pierres et vous tombez ensemble vers le sol,
ou si vous flottez tout librement dans l'espace.
Einstein réalisa que la gravité est
tellement insignifiante dans votre voisinage que
toutes les lois de la physique dans un petit référentiel
en chute libre doivent être les mêmes
que si vous vous déplaciez dans un Univers
sans gravité. En d'autres termes, un petit
référentiel en chute libre est "équivalent"
à un référentiel d'inertie
dans un Univers sans gravité. Les lois de
la physique sont identiques dans ces deux référentiels.
Einstein appela cela le principe d'équivalence.
De même, quand une cage d'ascenseur se décroche,
ses occupants se trouvent en état apparent
d'apesanteur. Tout se passe comme si la cage d'ascenseur
se trouvait en état de mouvement galiléen
ou inertiel. En effet, une chute ne peut être
distinguée d'un mouvement uniforme. On peut
alors imaginer que le mouvement est toujours uniforme
mais que la configuration de l'espace temps change,
ce qui engendre l'accélération du
champ gravitationnel. Ainsi, Einstein en conclut
que la gravitation avait pour effet de modifier
l'espace-temps. En se rapprochant du sol, les durées
et les distances s'étireraient de façon
à ce que la vitesse effective par rapport
à la "trame" de l'espace-temps
reste constante. C'est ce que l'on appelle la dérivée
covariante. La courbure de l'espace-temps est proportionnelle
à la densité de masse et d'énergie
locale, comme le montre l'équation d'Einstein
sur la loi de déformation de l'espace-temps.
L'équation d'Einstein : la loi de déformation
de l'Espace-Temps
La loi de déformation de l'espace-temps,
l'équation d'Einstein, stipule que "la
masse et la pression déforme l'espace-temps".
Plus précisément :
En tout point de l'espace-temps, on peu choisir
un référentiel arbitraire. Dans ce
référentiel, on peut explorer la courbure
de l'espace-temps en étudiant comment cette
courbure (force de marée) rapproche ou écarte
des particules libres dans les trois directions
de l'espace choisie (est-ouest, nord-sud, haut-bas).
Les particules suivent des géodésiques
de l'espace-temps et la vitesse à laquelle
elles se rapprochent ou s'écartent est proportionnelle
à la courbure dans la direction qui les relie.
Si elles se rapprochent comme dans les diagrammes
(a) et (b), on dit que la courbure est positive.
Si elles s'écartent comme dans le diagramme
(c), on dit que la courbure est négative.
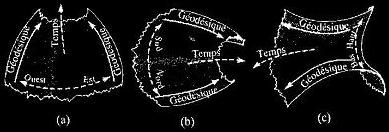
On additionne alors l'ampleur des courbures dans
les trois directions. L'équation d'Einstein
dit que la somme des ampleurs de ces courbures est
proportionnelle à la densité de masse
au voisinage de la particule (multiplié par
le carré de la vitesse de la lumière
pour la convertir en densité d'énergie)
augmentée de trois fois la pression de la
matière au voisinage de la particule.
Même si vous et moi sommes au même endroit
de l'espace-temps, si nous nous déplaçons
l'un par rapport à l'autre, votre espace
sera différent du mien, et de la même
façon la densité de masse (par exemple
la masse d'air autour de nous) que vous mesurerez
sera différente de la densité que
je mesurerai, et la pression (par exemple, la pression
de l'air) sera aussi différente. De la même
façon, la somme des trois courbures de l'espace-temps
que vous mesurerez sera différente de la
somme que je mesurerai. Mais vous et moi devrons
trouver que la somme des trois courbures que nous
mesurons est proportionnelle à la densité
de masse que nous mesurerons, augmentée de
trois fois la pression qu enous mesurerons. En ce
sens, l'équation d'Einstein est la même
dans tout référentiel : elle obéit
au principe de la Relativité.
Dans la plupart des cas (par exemple dans le système
solaire), la pression de la matière est minime
en comparaison de la densité de masse (multipliée
par le carré de la vitesse de la lumière,
et la pression contribue alors assez peu à
la courbure de l'espace-temps. La déformation
de l'espace-temps est alors essentiellement due
à la masse. Ce n'est qu'à l'intérieur
des étoiles à neutrons et dans quelques
autres endroits exotiques que la pression contribue
de façon importante à la déformation.
En manipulant mathématiquement son équation,
Einstein et les autres physiciens n'ont pas seulement
expliqué la déviation de la lumière
par le Soleil et le mouvement des planètes
sur leur orbite, ils ont aussi prédit l'existence
de trous noirs, de singularités dans l'espace-temps
et peut être même de trous de ver.
Plus la masse est concentrée, plus la courbure
de l'espace-temps est prononcée. Si nous
dessinons la trame de l'espace-temps sous la forme
d'un plan, nous pouvons de manière imagée
visualiser cette déformation. Dans le cas
d'un trou noir, la déformation n'a pas de
fin. Il y a une déchirure dans la trame de
l'espace-temps.

|
 |





